«Quien crea que el crecimiento exponencial puede durar eternamente en un mundo finito, o es un loco o es un economista». Kenneth Boulding (1918-1993), economista, presidente de la American Economic Association (1968).
Nunca se vio en
la naturaleza que una población o un organismo pudiera mantener su crecimiento
indefinidamente. Sólo a economistas se les puede ocurrir que los recursos
naturales son inagotables porque continuamente la tecnología, gracias al
estímulo del libre mercado, descubre nuevos recursos; no importa lo escasos que
lleguen a ser; cuanto más escasos, más subirá su precio, más ganará quien
descubra recursos alternativos, y antes se desarrollará la tecnología necesaria
para ello. Esta es la idea predicada por los neoliberales, dominante hasta
ahora en el pensamiento económico, irrefutable si sólo se razona en términos monetarios,
fácilmente desmontable si se razona en términos energéticos.
Está tan
arraigada la idea de la inevitabilidad del crecimiento que ya oficialmente se
habla del crecimiento sostenible como solución a la crisis, como si no eso no
fuera un oxymoron, una contradicción
en los términos. Esta gráfica sobre la previsión de las puntas de demanda
energética en la isla de Tenerife, sacada del documento del gobierno autónomo
de Canarias recientemente sometido a exposición pública “Revisión del Plan
Energético de Canarias PECAN 2006-2015”, es todo un ejemplo.
La línea recta
de pendiente positiva es prácticamente la única función matemática que maneja
el planificador oficial. Jamás veremos una recta en que a<0, ni siquiera una
línea horizontal donde y=cte. Toda previsión de futuro tiene inevitablemente
que ser creciente.
Los
planificadores son en el fondo personas sensatas. Aunque las directrices que
reciben les obligan a no considerar otra hipótesis más que la del crecimiento,
ellos por pudor se quedan en el crecimiento lineal, pero si sólo fuera por
quienes manejan verdaderamente la planificación, el crecimiento debería de ser
exponencial.
Por la propia
naturaleza crematística del sistema, todo capital invertido debe generar
plusvalía, y esa plusvalía se debe
reinvertir para seguir generando más plusvalía; toda cantidad prestada debe ser
devuelta con intereses, y los intereses generan a su vez más intereses. La
fórmula del interés compuesto es un caso particular de función exponencial.
Quien se lea la letra pequeña de cualquier contrato de préstamo que haya
firmado con su banco, se la encontrará.
Para que las
deudas se paguen tiene que haber crecimiento. Gran parte del trabajo y de los
recursos del mundo se destinan al crecimiento. Si el PIB de un estado no crece
al 3%, no se crea empleo, y debiera estar por el 8 o el 10% para que hubiera
pleno empleo. Un estado cuyo PIB “solo” crezca el 1% está en una grave crisis;
si decrece o se estanca, si no hay crecimiento, está en recesión: grave
situación que anuncia quiebras, paro, pobreza y conflictos sociales. El sistema
no funciona más que si la riqueza crece de forma exponencial.
En las épocas
en que la economía real no puede crecer exponencialmente, el dinero se refugia
en la economía virtual. Se especula con tulipanes, con solares, con opciones de
compra sobre solares, con casas, con contratos de futuros de materias primas,
con acciones, con pagarés, con fondos respaldados con hipotecas, con seguros
que respaldan a esos fondos, con papelitos de colores. Para ser especulador no
hace falta manejar grandes capitales, ni ser socio de la Trilateral, ni ser
invitado a las reuniones del Club Bilderberg. El señor que tiene los ahorros de
su vida o una modesta herencia puesta a plazo fijo al 2%, y dice que no le
renta nada, y lo pone en fondos de inversión que le rentan el 6% (que a su vez invierten
en sellos, trigo, petróleo o deuda emitida por el estado portugués), es un
especulador.
Las curvas de
crecimiento de la masa monetaria de USA (total de dólares, físicos o virtuales,
que ha emitido la Reserva Federal), y de su deuda externa (total de papelitos
de colores, físicos o virtuales, que USA le ha endosado al resto del mundo), que
no dependen para nada de la economía real ni de ningún impedimento físico, son
los mejores ejemplos que podemos poner de crecimiento exponencial sin límite.
En la
naturaleza se dan crecimientos exponenciales, pero sólo de forma temporal. Una
población, puesta en un medio donde no haya factores limitantes, primero se
multiplicará exponencialmente hasta que comience a agotar algún recurso
esencial; pasará por un punto de inflexión y aunque aún seguirá creciendo, lo
hará cada vez menos; llegará a un máximo, tras el cual decrecerá, primero
exponencialmente (como el que se cae por una pendiente), y luego tras un punto
de inflexión, caerá de forma cada vez más suave hasta llegar a un línea que
tienda a la horizontal.
Esa es la
función gaussiana. Cuando x sea igual b, la función alcanzará un máximo igual
a a. La forma de la curva dependerá
del parámetro c.
El crecimiento
de una población de bacterias dentro de un tubo de ensayo, el de los renos abandonados
en una isla del Artico sin ningún predador que controle su población, la evolución de la población en la isla de Pascua, todos los ecosistemas cerrados que no puedan autoregularse hasta llegar a un equilibrio siguen esta pauta de crecimiento.
La extracción de
un recurso no renovable en un yacimiento limitado sigue también una curva gaussiana.
Como comprobó el geólogo King Hubbert extrayendo petróleo en Estados Unidos
durante los años 50 (y podría corroborar cualquiera que haya extraido agua de un
pozo o de una galería), la pauta que sigue todo pozo de petróleo es que al
principio la producción crece de forma exponencial (cuanto más se perfora, más
se extrae), luego tiene a estabilizarse (cada vez cuesta más de extraer porque
hay que bombearlo desde mayor profundidad), hasta que la producción decrece por
mucho que se invierta en medios, primero abruptamente y luego menos, hasta su
total agotamiento. Sumando las curvas de producción de todos los pozos de
Estados Unidos, agotados o por agotar, obtuvo (evidentemente) una curva
gaussiana, de la que pudo deducir (conociendo los puntos de la parte izquierda de la curva) los valores de a, b y c en la fórmula
de la gaussiana anteriormente expuesta, y pudo predecir
correctamente en 1956 que el cenit de la producción de petróleo en Estados
Unidos se alcanzaría en torno a 1970.
Con idéntico
método la ASPO (Asociación de estudios del peak-oil) elaboró esta curva en 2004,
que predice el cenit de producción mundial de petróleo convencional para
mediados de la pasada década (ya ocurrió), y el del total de líquidos
(incluyendo el gas natural licuado) para el momento presente.
Ciertamente que la forma de esta gaussiana no es perfecta, porque los acontecimientos políticos afectan coyunturalmente al proceso, pero esos acontecimientos políticos están a su vez determinados por la geología. El doble pico en los años setenta corresponde a las crisis del petróleo de los años 1973, cuando la OPEP decretó un embargo contra los países que apoyaban a Israel en la guerra del Yom Kippur, y 1979, cuando la revolución islámica en Irán depuso al Sha. Nunca hubiera podido ser usado el petróleo como arma si antes en 1970 Estados Unidos (principal productor mundial hasta entonces) no hubiera llegado a su cenit de producción. No tendrían tanta trascendencia la actuales tensiones entre Irán y el imperio si Arabia Saudí, principal productor mundial y único que hasta ahora tenía capacidad excedentaria, no hubiera llegado recientemente a su cenit.
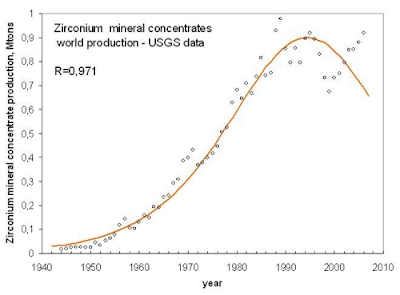
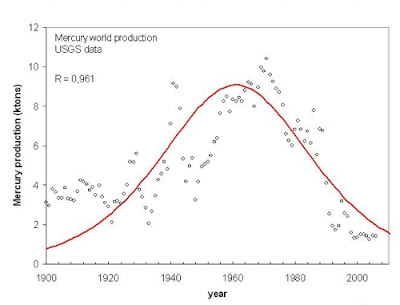
No sólo el petróleo. Todo tiene un pico, sobrepasado o próximo a sobrepasarse. Estas son las curvas previstas para la extracción del conjunto de petróleo y gas natural (pico en 2015), carbón (pico en 2025), uranio (pico en 2020), fosfatos (pico alcanzado en 1990), cobre (pico en 2020), oro (pico alcanzado en 2000), hierro, selenio, zirconio (picos alcanzados a mediados de los 90), plomo (pico alcanzado en 1990) y mercurio (pico alcanzado en los 60). De todo se puede sacar una gaussiana:
En un ecosistema donde todas las poblaciones lleguen finalmente a un equilibrio entre sí y con los recursos renovables de los que dependan, la población no tiene que tender a 0, sino que puede estabilizarse en muy un valor constante situado por encima.
En las simulaciones del World3, los escenarios desarrollistas a ultranza, donde no se hace nada por limitar la población ni la producción, acaban inevitablemente en colapso a medio plazo, independientemente de si los recursos también aumentan.
Los escenarios
donde se simula un esfuerzo real por limitar el crecimiento acaban, tras una
crisis temporal, con la población y los parámetros indicadores del nivel
material de vida estabilizados en valores relativamente altos.
Necesitamos que
comience a admitirse oficialmente que la Tierra no es plana e infinita, sino
esférica y limitada.





















No hay comentarios:
Publicar un comentario